ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Интегральное исчисление – это раздел математического анализа, в котором изучаются интегралы, их свойства, способы вычисления и приложения. Вместе с дифференциальным исчислением оно составляет основу аппарата математического анализа.
Даты возникновения некоторых математических знаков
| Знак | Значение | Кто ввел | Когда знак введен, год |
| Знаки объектов | |||
|
| бесконечность | Дж. Валлис | 1655 |
|
| отношение длины окружности к диаметру | У. Джонс Л. Эйлер | 1706 1736 |
|
| корень квадратный из | Л. Эйлер | 1777 |
|
| неизвестные или переменные величины | Р. Декарт | 1637 |
|
| вектор | О. Коши | 1853 |
| Знаки операций | |||
|
| сложение | немецкие математики | конец XV в. |
|
| вычитание | » | » |
|
| умножение | У. Оутред | 1631 |
|
| умножение | Г. Лейбниц | 1698 |
|
| деление | Г. Лейбниц | 1684 |
|
| степени | Р. Декарт | 1637 |
|
| корни | X. Рудольф А. Жирар | 1525 1629 |
|
| логарифм | И. Кеплер | 1624 |
|
| синус | Б. Кавальери | 1632 |
|
| косинус | Л. Эйлер | 1748 |
|
| тангенс | Л. Эйлер | 1753 |
|
| арксинус | Ж. Лагранж | 1772 |
|
| дифференциал | Г. Лейбниц | 1675 |
|
| интеграл | Г. Лейбниц | 1675 |
|
| производная | Г. Лейбниц | 1675 |
|
| определенный интеграл | Ж. Фурье | 1819-1822 |
|
| сумма | Л. Эйлер | 1755 |
|
| факториал | X. Крамп | 1808 |
|
| предел | У. Гамильтон многие математики | 1853 начало XX в. |
| | функция | И. Бернулли Л. Эйлер | 1718 1734 |
| Знаки отношений | |||
| | равенство | Р. Рекорд | 1557 |
| | больше меньше | Т. Гарриот | 1631 |
| | сравнимость | К. Гаусс | 1801 |
| | параллельность | У. Оутред | 1677 |
| | перпендикулярность | П. Эригон | 1634 |
Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них – физическая задача определения пройденного за данное время пути по известной, но, быть может, переменной скорости движения и значительно более древняя задача вычисления площадей и объемов геометрических фигур (см. Геометрические задачи на экстремум).
Центральным в интегральном исчислении является понятие интеграла, которое, однако, имеет две различные трактовки, приводящие соответственно к понятиям неопределенного и определенного интегралов.
В дифференциальном исчислении была введена операция дифференцирования функций. Рассматриваемая в интегральном исчислении обратная к дифференцированию математическая операция называется интегрированием или, точнее, неопределенным интегрированием.
В чем же состоит эта обратная операция и в чем ее неопределенность?
Операция дифференцирования сопоставляет заданной функции ее производную
. Допустим, что мы хотим, исходя из заданной функции
, найти такую функцию
, производной которой является функция
, т. е.
. Такая функция называется первообразной функции
.
Значит, обратная дифференцированию операция – неопределенное интегрирование – состоит в отыскании первообразной данной функции.
Заметим, что, наряду с функцией , первообразной для функции
, очевидно, будет также любая функция
, отличающаяся от
постоянным слагаемым
: ведь
.
Таким образом, в отличие от дифференцирования, сопоставлявшего функции единственную другую функцию – производную первой, неопределенное интегрирование приводит не к одной конкретной функции, а к целому набору функций, и в этом его неопределенность.
Однако степень этой неопределенности не так уж велика. Напомним, что если производная некоторой функции равна нулю во всех точках какого-то промежутка, то это функция, постоянная на рассматриваемом промежутке (на промежутках, где скорость изменения переменной величины везде равна нулю, она не меняется). Значит, если на каком-то промежутке
, то функция
постоянна на этом промежутке, поскольку ее производная
равна нулю во всех точках промежутка.
Итак, две первообразные одной и той же функции могут отличаться на промежутке только постоянным слагаемым.
Первообразные функции обозначают символом
,
где знак читается: интеграл. Это так называемый неопределенный интеграл. По доказанному, неопределенный интеграл изображает на рассматриваемом промежутке не одну конкретную функцию, а любую функцию вида
, (1)
где - какая-то первообразная функции
на данном промежутке, а
- произвольная постоянная.
Например, на всей числовой оси
;
;
.
Мы здесь специально обозначили аргументы подынтегральных функций различными символами: ![]() , чтобы обратить внимание на независимость первообразной как функции от выбора буквы, используемой для обозначения ее аргумента.
, чтобы обратить внимание на независимость первообразной как функции от выбора буквы, используемой для обозначения ее аргумента.
Проверка написанных равенств выполняется простым дифференцированием их правых частей, в результате которого получаются стоящие в левых частях под знаком интеграла функции ,
,
соответственно.
Полезно иметь в виду также следующие очевидные соотношения, непосредственно вытекающие из определений первообразной, производной, дифференциала и из соотношения (1) для неопределенного интеграла:
,
,
,
.
Отыскание первообразной часто облегчают некоторые общие свойства неопределенного интеграла:
(вынесение постоянного множителя);
(интегрирование суммы); если
,
то
(замена переменной).
Эти соотношения также проверяются непосредственно с использованием соответствующихправил дифференцирования.
Найдем закон движения свободно падающего в пустоте тела, исходя из единственного факта, что при отсутствии воздуха ускорение свободного падения вблизи поверхности Земли постоянно и не зависит от особенностей падающего тела. Фиксируем вертикальную координатную ось; направление на оси выберем в сторону к Земле. Пусть
- координата нашего тела в момент
. Нам известно, таким образом, что
и
- постоянная. Требуется найти функцию
- закон движения.
Поскольку , где
, то, последовательно интегрируя, находим
(2)
Итак, мы нашли, что
, (3)
где и
- какие-то постоянные. Но падающее тело подчиняется все-таки одному конкретному закону движения, в котором уже нет никакого произвола. Значит, есть еще какие-то условия, которые мы пока не использовали; они позволяют среди всех «конкурирующих» законов (3) выбрать тот, который соответствует конкретному движению. Эти условия легко указать, если разобраться в физическом смысле постоянных
и
. Если сравнить крайние члены соотношения (2) при
, то выяснится, что
, а из (3) при
получается, что
. Таким образом, математика сама напомнила нам, что искомый закон движения
вполне определится, если указать начальное положение и начальную скорость
тела. В частности, если
и
, получаем
.
Отметим теперь, что между операцией нахождения производной (дифференцированием) и операцией отыскания первообразной (неопределенным интегрированием) имеется, кроме указанного выше, еще целый ряд принципиальных отличий. В частности, следует иметь в виду, что если производная любой комбинации элементарных функций сама выражается через элементарные функции, т.е. является элементарной функцией, то первообразная элементарной функции уже не всегда является функцией элементарной. Например, первообразная
элементарной функции (называемая интегральным синусом и обозначаемая специальным символом
), как можно доказать, не выражается в элементарных функциях. Таким образом, принципиальный математический вопрос о существовании первообразной у наперед заданной функции не надо смешивать с не всегда разрешимой задачей об отыскании этой первообразной среди элементарных функций. Интегрирование часто является источником введения важных и широко используемых специальных функций, которые изучены ничуть не хуже таких «школьных» функций, как
или
, хотя и не входят в список элементарных функций.
Наконец, отметим, что отыскание первообразной, даже когда она выражается в элементарных функциях, скорее напоминает искусство, чем канонический алгоритм вычислений, подобный алгоритму дифференцирования. По этой причине найденные первообразные наиболее часто встречающихся функций собраны в виде справочных таблиц неопределенных интегралов. Следующая микротаблица такого рода, очевидно, равносильна микротаблице производных соответствующих основных элементарных функций:
Мы, пока говорили об обращении операции дифференцирования, пришли в этой связи к понятиям первообразной, неопределенного интеграла и дали первоначальное определение этих понятий.
Теперь укажем иной, куда более древний подход к интегралу, который послужил основным первоначальным источником интегрального исчисления и привел к понятию определенного интеграла или интеграла в собственном смысле этого слова. Этот подход четко прослеживается уже у древнегреческого математика и астронома Евдокса Книдского (примерно 408-355 до н.э.) и Архимеда, т.е. он возник задолго до появления дифференциального исчисления и операции дифференцирования.
Вопрос, который рассматривали Евдокс и Архимед, создав при его решении «метод исчерпывания», предвосхитивший понятие интеграла – это вопрос о вычислении площади криволинейной фигуры. Ниже мы рассмотрим этот вопрос, а пока поставим, вслед за И. Ньютоном, следующую задачу: по известной в любой момент из промежутка времени
скорости
тела найти величину перемещения тела за этот промежуток времени.
Если бы был известен закон движения, т.е. зависимость координаты тела от времени, то ответ, очевидно, выражался бы разностью . Более того, если бы мы знали какую-либо первообразную
функции
на промежутке
, то, поскольку
, где
- постоянная, можно было бы найти искомую величину перемещения в виде разности
, которая совпадает с разностью
. Это очень полезное наблюдение, однако если первообразную данной функции
указать не удается, то действовать приходится совсем иначе.
Будем рассуждать следующим образом.
Если промежуток отдельными моментами
, такими, что
, разбить на очень мелкие временные промежутки
,
, то на каждом из этих коротких промежутков скорость
тела не успевает заметно измениться. Фиксировав произвольно момент
, можно таким образом приближенно считать, что на промежутке времени
движение происходит с постоянной скоростью
. В таком случае для величины пути, пройденного за промежуток времени
, получаем приближенное значение
, где
. Складывая эти величины, получаем приближенное значение
(4)
для всего перемещения на промежутке .
Найденное приближенное значение тем точнее, чем более мелкое разбиение промежутка мы произведем, т.е. чем меньше будет величина
наибольшего из промежутков
, на которые разбит промежуток
.
Значит, искомая нами величина перемещения есть предел
(5)
сумм вида (4), когда величина стремится к нулю.
Суммы специального вида (4) называются интегральными суммами для функции на промежутке
, а их предел (5), получаемый при неограниченном мельчании разбиений, называется интегралом (илиопределенным интегралом) от функции
на промежутке
. Интеграл обозначается символом
,
в котором числа называются пределами интегрирования, причем
- нижним, a
- верхним пределом интегрирования; функция
, стоящая под знаком
интеграла, называется подынтегральной функцией;
- подынтегральным выражением;
- переменной интегрирования.
Итак, по определению,
. (6)
Значит, искомая величина перемещения тела за временной промежуток при известной скорости
движения выражается интегралом (6) от функции
по промежутку
.
Сопоставляя этот результат с тем, который на языке первообразной был указан в начале рассмотрения этого примера, приходим к знаменитому соотношению:
, (7)
если . Равенство (7) называется формулой Ньютона-Лейбница. В левой его части стоит понимаемый как предел (6) интеграл, а в правой – разность значений (в концах
и
промежутка интегрирования) функции
, первообразной подынтегральной функции
. Таким образом, формула Ньютона-Лейбница связывает интеграл (6) и первообразную. Этой формулой можно, следовательно, пользоваться в двух противоположных направлениях: вычислять интеграл, найдя первообразную, или получать приращение первообразной, найдя из соотношения (6) интеграл. Мы увидим ниже, что оба эти направления использования формулы Ньютона-Лейбница весьма важны.
Интеграл (6) и формула (7) в принципе решают поставленную в нашем примере задачу. Так, если (как это имеет место в случае свободного падения, начинающегося из состояния покоя, т.е. с
), то, найдя первообразную
функции
по формуле (7), получаем величину
перемещения за время, прошедшее от момента до момента
.
На основе разобранной только что физической задачи, приведшей нас к интегралу и формуле Ньютона-Лейбница, обобщая сделанные наблюдения, можно теперь сказать, что если на некотором промежутке задана функция
, то, разбивая промежуток
точками
, составляя интегральные суммы
, (4')
где ,
, и переходя к пределу при
, где
, мы получаем по определению интеграл
(6')
от функции по промежутку
. Если при этом
на
, т.е.
- первообразная функции
на промежутке
, то имеет место формула Ньютона-Лейбница:
. (7)
 Получите свидетельство
Получите свидетельство Вход
Вход



 , где {\displaystyle m}
, где {\displaystyle m} и {\displaystyle n}
и {\displaystyle n} натуральные числа. Для такого прямоугольника можно подобрать такой «единичный квадратик», который полностью покроет такой прямоугольник. Сторону «единичный квадратик» можно подобрать как d = НОД(m, n), где {\displaystyle d}
натуральные числа. Для такого прямоугольника можно подобрать такой «единичный квадратик», который полностью покроет такой прямоугольник. Сторону «единичный квадратик» можно подобрать как d = НОД(m, n), где {\displaystyle d} — натуральное число. Например, если мы имеем прямоугольник длиной 10 см и шириной 14 см, то такой прямоугольник может быть построен при помощи циркуля и линейки (если длину принять за единицы, его ширина будет 14 / 10 = 7/5). В качестве стороны «единичного квадратика» можно взять d = НОД(14, 10) = 2 см. Этот квадратик войдёт 5 раз в длину и 7 в ширину, всего нужно 5 × 7 = 35 таких «единичных квадратиков». Можно взять квадраты со стороной 1 см. Этот квадратик войдёт 10 раз в длину и 14 в ширину, всего нужно 10 × 14 = 140 таких «единичных квадратиков». Из этого построения видно, что размерность (см.) не играет никакой существенной роли при таком построении.
— натуральное число. Например, если мы имеем прямоугольник длиной 10 см и шириной 14 см, то такой прямоугольник может быть построен при помощи циркуля и линейки (если длину принять за единицы, его ширина будет 14 / 10 = 7/5). В качестве стороны «единичного квадратика» можно взять d = НОД(14, 10) = 2 см. Этот квадратик войдёт 5 раз в длину и 7 в ширину, всего нужно 5 × 7 = 35 таких «единичных квадратиков». Можно взять квадраты со стороной 1 см. Этот квадратик войдёт 10 раз в длину и 14 в ширину, всего нужно 10 × 14 = 140 таких «единичных квадратиков». Из этого построения видно, что размерность (см.) не играет никакой существенной роли при таком построении.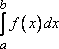









 Интегральное исчисление (398.52 KB)
Интегральное исчисление (398.52 KB)
 0
0 465
465 8
8 Нравится
0
Нравится
0


