Решение систем линейных уравнений с помощью матриц

Решение систем линейных уравнений с помощью матриц

МАТРИЦЫ

Понятие матрицы впервые появилось в середине XIX в. в работах У.Гамильтона и А.Кели. Фундаментальные результаты в теории матриц принадлежат К.Вейерштрассу, К.Жордану.

Матрица – это таблица чисел, составленная определенным образом.

Виды матриц

• Прямоугольная матрица m ≠ n
• Квадратная матрица m = n

2 1 3 4 5 6

1 2 3 1 -1 0

А =

3 1 2

4 -1 0

1 3 5

В =

Существуют и другие виды матриц:

• Матрица-строка (m = 1)

А = ( a11 a12 … an)

• Матрица-столбец (n = 1)

• Нуль-матрица

а 11

а 12

…

а 1m

A =

0 0 … 0

0 0 … 0

…………

0 0 … 0

A =

А т = " width="640"

• Единичная матрица
• Транспонированная матрица

1 0 0

0 1 0

0 0 1

I =

а 11 а 21

а 12 а 22

а 13 а 23

а 11 а 12 а 13

а 21 а 22 а 23

A =

=

А т =

• Присоединенная матрица

А 11 А 12 А 13

А 21 А 22 А 23

А 31 А 32 А 33

А =

, A 12 = -

A 11 =

a 21 a 23

a 31 a 33

a 22 a 23

a 32 a 33

, … , A 33 =

a 11 a 12

a 21 a 22

ДЕЙСТВИЯ НАД МАТРИЦАМИ

умножение

а 11 а 12

а 21 а 22

b 11 b 12 b 13

b 21 b 22 b 23

А ∙ В =

∙

=

а 11 b 11 +а 12 b 21 а 11 b 12 +а 12 b 22 а 12 b 13 +а 12 b 23

а 21 b 11 +а 22 b 21 а 21 b 12 +а 22 b 12 а 21 b 13 +а 21 b 23

ОБРАТНАЯ МАТРИЦА

Определение : Матрица А -1 называется обратной по отношению к матрице А , если выполнено равенство:

А А -1 = А -1 А = I ,

где I – единичная матрица.

Обратная матрица А -1 находиться по следующему правилу:

А 11 А 21 А 31

А 12 А 22 А 32

А 13 А 23 А 33

1

det A

А -1 =

а 11 а 12 а 13

∆ = а 21 а 22 а 23

а 31 а 32 а 33

а11 а22 а33 - главная диагональ

а 13 а22 а31 - побочная диагональ

«Звездочка»

а 11 а 12 а 13

∆ = а 21 а 22 а 23 =

а 31 а 32 а 33

а 11 ∙ а 22 ∙ а 33 + а 12 ∙ а 23 ∙ а 31 + а 21 ∙ а 32 ∙ а 13 –

- (а 31 ∙ а 22 ∙ а 13 + а 21 ∙ а 12 ∙ а 33 + а 32 ∙ а 23 ∙ а 11 )

Способ вычисления определителя через алгебраические дополнения

а 11 а 12 а 13

∆ = а 21 а 22 а 23 =

а 31 а 32 а 33

= А 11 = а 22 а 23 - А 12 = а 21 а 23 +

а 32 а 33 а 31 а 33

А 13 = а 21 а 22

а 31 а 32

Габриел ь Крамер

(1704-1752)

МЕТОД КРАМЕРА

a). Если  , то система

имеет единственное решение, которое может быть найдено по формулам Крамера :

где определитель n-го порядка  i ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b 1 , b 2 ,..., b n .

a 11 x 1 +a 12 x 2 +a1 3 x 3 +…a 1n x n =b 1 a 21 x 1 +a 22 x 2 +a 23 x 3 +…a 2n x n =b 2 ………………………………………… a m1 x 1 +a m2 x 2 +a m3 x 3 +…a mn x n =b m

х 1 =

∆ 1

, х 2 =

∆

∆ 2

, х i =

∆

∆ i

∆

б). Если  , то система

либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.

a 11 x 1 +a 12 x 2 +a1 3 x 3 +…a 1n x n =b 1 a 21 x 1 +a 22 x 2 +a 23 x 3 +…a 2n x n =b 2 ……………………………………………… a m1 x 1 +a m2 x 2 +a m3 x 3 +…a mn x n =b m

Алгоритм решения

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

1. В данной системе составим главный определитель и вычислим.

2. Составить и вычислить следующие определители :

3. Воспользоваться формулами Крамера.

Пример:

Ответ: x=0,5 ; y=2 ; z=1,5 .

Гаусс Карл Фридрих

(30.4.1777-23. 2. 1855)

Поясним смысл метода Гаусса на системе четырёх уравнений с четырьмя неизвестными.

a11x + a12y + a13z + a14u = a1 (a)

a21x + a22y + a23z + a24u = a2 ( б )

a31x + a32y + a33z + a34u = a3 ( в )

a41x + a42y + a43z + a44u = a4 ( г )

Допустим, что а = 0 ( если а = 0, то изменим порядок уравнений, в котором коэффициент при x = 0)

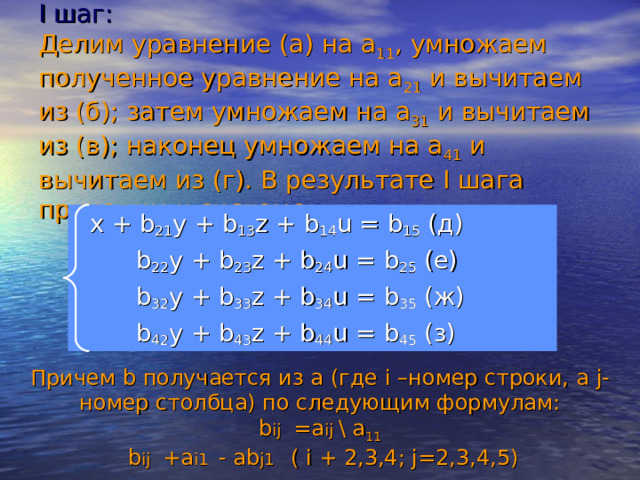
I шаг: Делим уравнение (а) на а 11 , умножаем полученное уравнение на а 21 и вычитаем из (б); затем умножаем на а 31 и вычитаем из (в); наконец умножаем на а 41 и вычитаем из (г). В результате I шага приходим к системе:

x + b 21 y + b 13 z + b 14 u = b 15 (д)

b 22 y + b 23 z + b 24 u = b 25 (е)

b 32 y + b 33 z + b 34 u = b 35 (ж)

b 42 y + b 43 z + b 44 u = b 45 (з)

Причем b получается из а (где i –номер строки, а j - номер столбца) по следующим формулам:

b ij = a ij \ a 11

b ij +a i1 - ab j1 ( i + 2,3,4; j=2,3,4,5)

I I шаг: Поступаем с уравнениями (е) ,(ж) ,(з) точно так же , как с уравнениями (а), (б), (в),(г). В итоге исходная система преобразуется к так называемому ступенчатому виду:

x + b12y + b13z + b14u =b15 ( д )

b22y + b23z + b24u =b25 ( е )

b32y + b33z + b34u =b35 ( ж )

b42y + b43z + b44u =b45 (з)

Из преобразованной системы все неизвестные определяются последовательно, без труд.

система совместна 1 3 -2 имеет единственное решение) ∆ = " width="640"

Пример: Решить систему уравнений

х 1 + х 2 – 0,5х 3 = 2

3х 1 – х 2 – 3х 3 = 7

х 1 + 3х 2 – 2х 3 = 3

1 1 -0,5

3 -1 -3 = 9 (∆ ≠ 0 = система совместна

1 3 -2 имеет единственное решение)

∆ =

1 1 -0,5 2

3 -1 -3 7

1 3 -2 3

1 1 -0,5 2

0 -4 -1,5 1

0 -2 1,5 -1

A =

~

~

1 1 -0,5 2

0 -4 -1,5 1

0 0 4,5 3

~

Вернёмся к системе:

х1 + х2 – 0,5х3 = 2 х3 = -2/3

-4х2 -1,5х3 = 1 х2 = 0

-4,5х = 3 х1 = 5\3

Ответ: 5/3; 0; -2/3

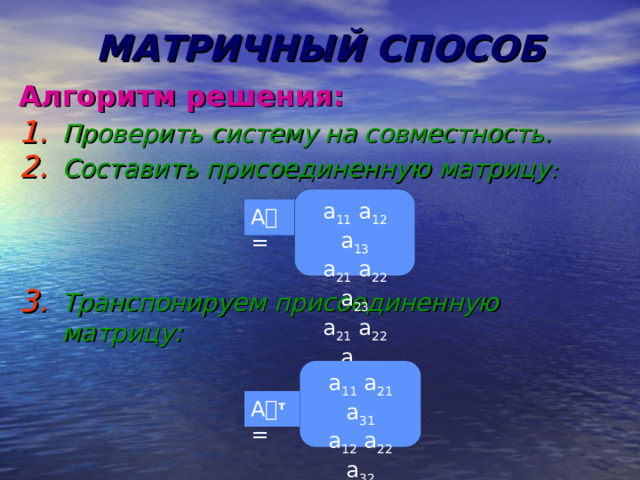
МАТРИЧНЫЙ СПОСОБ

Алгоритм решения:

• Проверить систему на совместность.
• Составить присоединенную матрицу :

• Транспонируем присоединенную матрицу:

а 11 а 12 а 13

а 21 а 22 а 23

а 21 а 22 а 23

А =

а 11 а 21 а 31

а 12 а 22 а 32

а 13 а 23 а 33

А т =

• Составим обратную матрицу:
• Итог решения:

X = A -1 ∙ В

а 11

∆

a 21

a 12

∆

∆

a 31

a 22

a 13

∆

∆

∆

a 23

a 32

∆

∆

a 33

∆

А -1 =

Задача

Мы за время летних каникул заработали 100 тысяч рублей. В банке, где мы решили поместить свои деньги на самых выгодных условиях, мы узнали о наличии особого вида сбережения – математического счета. Для таких счетов банк гарантирует свой обычный процент на момент открытия счета в двукратном размере при условии, если вкладчик разделит определенным образом свой вклад на три части в трех отделениях банка, если же вкладчик не сможет этого сделать, он получит обычный процент.

Условия банка следующие: разделить вклад на три части в отделениях банка А, Б, В так, чтобы

• величина вклада в отделении Б равнялось сумме величины вклада в отделении А и удвоенной величины вклада в отделении В;
• величина вклада в отделении В равнялось сумме удвоенной величины вклада в отделении А и утроенной величины вклада в отделении Б;
• утроенная величина вклада в отделении А равнялось сумме удвоенной величины вклада в отделении Б и утроенной величины вклада в отделении В.

система совместна и имеет единственное решение. 2. Найдем следующие определители: ∆ х = 0, ∆ y = 0, ∆ z = 0 3. По формуле Крамера найдем х, у, z x = 0, y = 0, z = 0 " width="640"

РЕШЕНИЕ ЗАДАЧИ

Составим систему уравнении согласно условиям, предложенные банком, где сумма денег в ячейке А = х, Б = y и В = z :

4 = x + 2 z

z = 2 x + 3 y

3 x = 2 y + 3 z

Преобразуем уравнения системы:

x – y + 2 z = 0

2 x + 3 y – z = 0

3 x – 2 y – 3 z = 0

Данную систему решим методом Крамера:

1. Найдем главный определитель:

∆ =

-40

∆ х =

0 -1 2

0 3 -1

0 -2 -3

= 0

∆ ≠ 0 = система совместна и имеет единственное решение.

2. Найдем следующие определители:

∆ х = 0, ∆ y = 0, ∆ z = 0

3. По формуле Крамера найдем х, у, z

x = 0, y = 0, z = 0