Изучив данный учебный элемент, Вы узнаете:
Определение неопределенного интеграла.
Таблицу вычисления основных неопределенных интегралов.
Правила интегрирования неопределенных интегралов.
Оборудование, материалы и вспомогательные средства:
персональный компьютер;
мультимедиа проектор;
презентация урока;
Сопутствующие учебные элементы и пособия:
1. Учебник «А.Г. Мордкович «Алгебра и начала анализа 10-11 классы»
2. Задачник «А.Г. Мордкович «Алгебра и начала анализа 10-11 классы»
Задача отыскания первообразной для заданной функции у = f(х) имеет не одно решение. Рассмотрим этот вопрос более детально.
Запись в тетрадь:
Теорема. Если y=F(x)— первообразная для функции у = f(х) на промежутке X , то у функции у = f(х) бесконечно много первообразных и все они имеют вид y=F(x)+С.
Доказательство. 1. Пусть y=F(x) -первообразная для функции у = f(х) на промежутке X . Это значит, что для всех х из X выполняется равенство F'(x)=f(x). Найдем производную любой функции вида y=F(x)+С :
(F(x)+C)'=F'(x)+C'=f(x)+0=f(x)
Итак, (F(x)+C)'=f(x)
Это значит, что y=F(x)+С является первообразной для функции у = f(х) .
Таким образом, мы доказали, что если у функции у = f(х) есть первообразная y=F(x) , то у функции у = f(х) бесконечно много первообразных: например, любая функция вида y=F(x)+С является первообразной.
2. Докажем теперь, что указанным видом функций исчерпывается все множество первообразных.
Пусть y=F1 (x) и y=F(x) — две первообразные для функции у = f(х) на промежутке X. Это значит, что для всех х из X выполняются соотношения F '1 (x) = f(х) и F ' (x) = f(х).
Рассмотрим функцию у = H(х), где H(х) = F 1 (x)- F (x) , и найдем ее производную: (H(x))'=(F 1 (x)- F(x))' = F'1 (x)-F'(x) = f(x)-f(x) =0
Известно, что если производная функции у = H(х) на промежутке X тождественно равна нулю, то функция постоянна на промежутке X .
Значит, H(x)=C , т.е. F1 (x)-F(x)=C , F1
Теорема доказана.
Запись в тетрадь:
Определение . Если функция у = f(х) имеет на промежутке X первообразную y=F(x) , то множество всех первообразных, т. е. множество функций вида y=F(x)+С , называют неопределенным интегралом от функции у = f(х) и обозначают

Весь материал - смотрите документ.
 Получите свидетельство
Получите свидетельство Вход
Вход



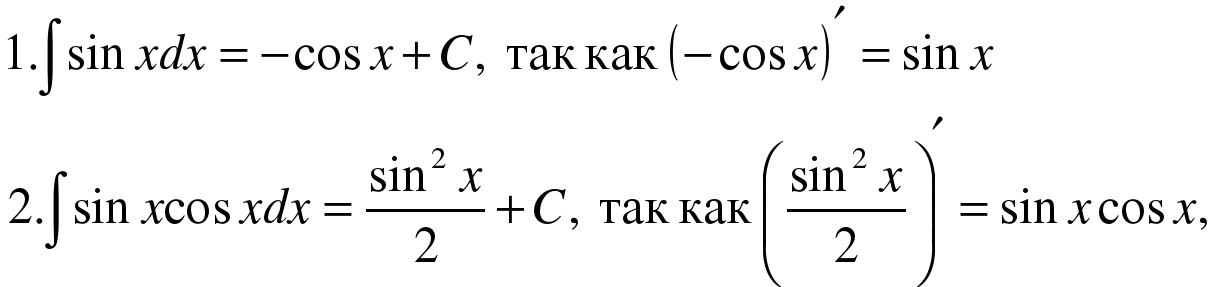









 Учебный элемент по математике "Неопределенный интеграл" (0.13 MB)
Учебный элемент по математике "Неопределенный интеграл" (0.13 MB)
 0
0 355
355 7
7 Нравится
0
Нравится
0


