Всё время, пока существует волна, частицы среды совершают колебания около своих положений равновесия и смещаются от него не более чем на амплитуду. При этом различные частицы колеблются со сдвигом по фазе, за исключением тех, положения равновесия которых находятся друг от друга на расстоянии υТ.
Напомним, что геометрическое место точек среды, колеблющихся в одинаковых фазах, образует волновую поверхность.
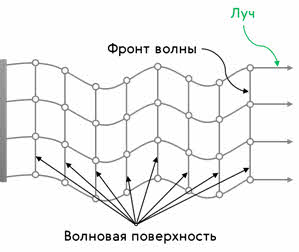
Волновую поверхность, отделяющую колеблющиеся частицы среды от частиц, ещё не начавших колебаться, называют фронтом волны.
Как отмечалось нами ранее, возмущение, создаваемое источником волны, передаётся от одной точки среды к другой не мгновенно, а с определённой конечной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени.
Для указания направления распространения волн, используется понятие луча. Лучом мы будем называть линию, проведённую перпендикулярно волновому фронту в направлении распространения волны.
Ранее мы с вами показали, что при возбуждении волны происходит процесс распространения колебаний, но не перенос вещества. Следовательно, при распространении волн происходит перенос энергии упругой деформации и импульса без переноса вещества. При этом энергия волны в упругой среде состоит из кинетической энергии совершающих колебания частиц и потенциальной энергии упругой деформации среды.
На прошлом уроке мы с вами говорили о том, что расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны. Она равна тому расстоянию, на которое распространяется волна за период:
λ = υT.
Так как период колебаний обратно пропорционален частоте колебаний, то скорость волны связана с частотой колебаний уравнением:
υ = λν.
Выразим из этой формулы длину волны, а также воспользуемся связью частоты колебаний с их циклической частотой:

Отсюда видно, что при возникновении волн в среде их частота определяется частотой колебаний источника. А скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.
Теперь давайте получим уравнение плоской волны, то есть волны, волновые поверхности которой представляют собой плоскости, перпендикулярные к направлению распространения волны.
Предположим, что вибратор совершает гармонические колебания, подчиняющиеся закону синуса (считаем, что начальная фаза колебаний равна нулю):

В записанной формуле s — это смещение колеблющейся точки от положения равновесия, а sm — амплитуда колебаний.

В точках, отстоящих на расстоянии х от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать от колебаний источника на время:

Эти точки также начнут также совершать гармонические колебания с той же частотой, но с запаздыванием на время τ. Колебания в точке х будут происходить с той же амплитудой, но с другой фазой:

Это и есть уравнение плоской бегущей монохроматической волны. При этом считают, что в процессе распространения волны её затуханием можно пренебречь. Из уравнения видно, что смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени и расстояния до равновесного положения точки среды.
Из этого уравнения также следует, что амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника. Также видно, что любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления данной точки от источника колебаний:

А положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением, которое вы сейчас видите на экране:

Здесь «Бета» (β) — это величина, зависящая от времени.

На экране вы видите график этой функции в начальный момент времени — график волны. Он представляет собой как бы «моментальный» снимок волны в данный момент времени. График волны, в отличие от графика колебаний, который показывает зависимость смещения одной частицы от времени в данной точке среды, показывает зависимость смещения всех частиц среды из положения равновесия от расстояния до источника колебаний в некоторый фиксированный момент времени.
А теперь давайте с вами найдём разность фаз колебаний двух точек среды, находящихся на некотором расстоянии друг от друга:

Запишем уравнения, описывающие колебания этих двух точек:

Теперь найдём их разность фаз (напомним, что фазой колебания является аргументом периодической функции):

Перепишем полученное уравнение, воспользовавшись формулой, связывающей циклическую частоту с периодом колебаний:
В знаменателе формулы мы получили произведение периода колебаний и скорости волны, а это, как мы помним, есть длина волны:

Из последнего равенства следует, что если две точки находятся друг от друга на расстоянии длины волны, то разность фаз колебаний этих точек равна 2π, что соответствует данному нами ранее определению длины волны.
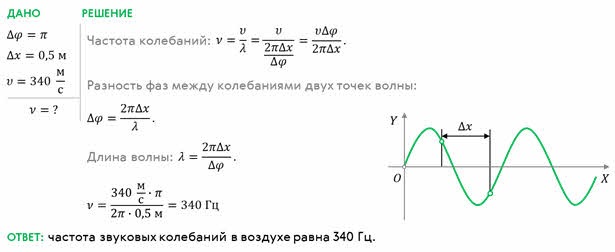
Теперь, для закрепления нового материала, давайте решим с вами задачу. Определите частоту звуковых колебаний в воздухе, если расстояние между двумя ближайшими точками волны, отличающимися по фазе на π, составляет 50 см. Для удобства будем считать, что скорость звука равна 340 м/с.
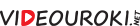
 Получите свидетельство
Получите свидетельство Вход
Вход




 6855
6855

